《概率论与数理统计》(本科4学时考试)教学大纲
来源:Betway必威 时间:2022-06-16 点击数:
《概率论与数理统计》(本科4学时考试)教学大纲
课程名称(汉):《概率论与数理统计》(本科4学时考试)
课程名称(英):Probability Theory and Mathematical Statistics
课程代码:112160051
课程类型:学科基础平台大类基础课程模块
适用对象:信息工程学院计算机科学与技术、电子信息科学与技术、通信工程、物联网工程专业; 人工智能学院自动化大学二年级本科
学时/学分:64学时/4学分
先修课程:《高等数学》、《线性代数》
方案版本:2022版
一、课程简介
《概率论与数理统计》是研究随机现象统计规律性的数学学科,在高等学校教学计划中是一门重要的基础理论课。概率论是对随机现象统计规律演绎的研究,而数理统计是对随机现象统计规律归纳的研究。虽然两者在方法上是如此明显的不同,但作为一门学科他们却互相渗透、互相联系。许多兴起的应用数学,如信息论、对策论、排队许多兴起的应用数学,如信息论、对策论、排队论、控制论等,都是以概率论作为基础的。数理统计在自然科学、工程技术、管理科学及人文社会科学中也有深刻、广泛的应用,其研究的内容也随着科学技术和政治、经济与社会的不断发展而逐步扩大。
二、课程的教学目标
通过本课程的学习,使学生了解概率论与数理统计的基本概念,掌握概率论与数理统计的基本理论,从而使学生初步掌握处理随机现象的基本思想和方法,培养学生运用概率统计方法解决实际问题的能力。
三、课程目标对××专业毕业要求的支撑关系
毕业要求 |
毕业要求指标点(非认证专业可以省略本项内容) |
课程目标 |
支撑权重 |
|
|
|
|
|
|
|
|
|
|
|
|
四、教学内容及其基本要求
序号 |
教学内容 |
教学要求(包括重点难点、教学方法、学生掌握的程度等) |
对应课程目标 |
1 |
概率论的基本概念 |
了解样本空间的概念,理解随机事件的定义,掌握事件的关系及运算;理解概率、条件概率的概念,掌握概率的基本性质,会计算古典型概率和几何型概率;掌握概率的加法公式、乘法公式、全概率公式、贝叶斯公式;理解事件独立性的概念,掌握用事件独立性进行概率计算的方法,理解独立性重复试验的概念,掌握计算有关事件概率的方法。 教学重点:概率的概念,用集合的概念理解事件、计算概率。 教学难点:条件概率与独立性,全概率公式与贝叶斯公式。 教学方法:讲授教学法、启发引导式教学法、讨论式教学法、习题讲解式教学法。 |
透彻地理解随机变量的定义,会计算事件的概率。 |
2 |
随机变量 |
理解随机变量的概念;理解随机变量的分布函数的概念和性质;理解离散型随机变量及其分布律的概念,掌握0-1分布、二项分布、泊松分布及其应用,会用泊松分布近似表示二项分布;理解连续型随机变量及其概率密度的概念,掌握均匀分布、指数分布和正态分布及其应用;会求随机变量函数的分布。 教学重点:离散型随机变量分布律,二项分布,泊松分布;连续型随机变量及其概率密度,正态分布的相关计算;离散型随机变量函数的分布。 教学难点:随机变量分布函数,连续型随机变量函数的概率密度定理。 教学方法:讲授教学法、启发引导式教学法、讨论式教学法、习题讲解式教学法。 |
把随机事件的计算从集合转移到函数这个工具上来,掌握一维随机变量的分布函数、概率密度的计算方法。 |
3 |
多维随机变量 |
掌握二维随机变量的联合分布函数的性质;掌握二维离散型随机变量的联合分布律及其性质,二维连续型随机变量的联合概率密度及其性质;理解边缘分布的概念,掌握两个随机变量联合分布的边缘分布;理解二维离散型随机变量的条件分布律,二维连续型随机变量的条件分布;理解随机变量独立性的概念,掌握离散型和连续型随机变量独立的条件;会求两个随机变量简单函数的分布。 教学重点:二维随机变量及其分布,两个随机变量独立性的概念。 教学难点:连续型随机变量的边缘密度函数,条件概率,二维连续型随机变量函数的分布。 教学方法:讲授教学法、启发引导式教学法、讨论式教学法、习题讲解式教学法。 |
使学生掌握二维随机变量及其分布的计算方法。 |
4 |
随机变量的数字特征 |
理解随机变量数字特征(期望、方差、标准差、协方差、相关系数)的概念。掌握数字特征的性质与计算。掌握常用随机变量分布的数字特征。会计算一维、二维随机变量函数的数学期望和方差。 教学重点:随机变量数字特征的计算。 教学难点:二维随机变量的协方差和相关系数。 教学方法:讲授教学法、启发引导式教学法、讨论式教学法、习题讲解式教学法。 |
使学生掌握随机变量的数字特征及其计算方法。 |
5 |
大数定律与中心极限定理 |
了解切比雪夫不等式。了解切比雪夫大数定律,伯努利大数定律和辛钦大数定律;了解独立同分布的中心极限定理和棣莫弗-拉普拉斯定理的结论和应用条件,并会用相关定理近似计算有关事件的概率。 教学重点:利用中心极限定理进行相关计算。 教学难点:三个大数定律。 教学方法:讲授教学法、启发引导式教学法、讨论式教学法、习题讲解式教学法。 |
使学生掌握用切比雪夫不等式和中心极限定理计算事件概率的方法。 |
6 |
数理统计的基本概念 |
理解总体、简单随机样本、统计量、样本均值、样本方差及样本矩的概念;了解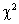 分布、 分布、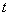 分布和 分布和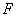 分布的定义及性质,了解分位数的概念,并会查相应的数值表;掌握正态总体的样本均值、样本方差及样本矩的抽样分布。 分布的定义及性质,了解分位数的概念,并会查相应的数值表;掌握正态总体的样本均值、样本方差及样本矩的抽样分布。 教学重点:统计量的定义及常用统计量的计算。 教学难点:正态总体的抽样分布。 教学方法:讲授教学法、启发引导式教学法、讨论式教学法、习题讲解式教学法。 |
使学生理解数理统计中的基本概念,并掌握常见统计量及抽样分布。 |
7 |
参数估计 |
理解参数的点估计和区间估计的概念;熟练掌握矩估计法和极大似然估计法;掌握估计量的评价标准(无偏性、有效性、一致性)的概念,能验证估计量的无偏性; 了解区间估计的概念,会求单个正态总体中一个或两个未知参数的置信区间。 教学重点:矩估计法和极大似然估计法。 教学难点:极大似然估计法,单个正态总体的区间估计。 教学方法:讲授教学法、启发引导式教学法、讨论式教学法、习题讲解式教学法。 |
使学生掌握点估计和区间估计的原理和计算方法。 |
8 |
假设检验 |
掌握显著性检验的基本思想、基本步骤;了解假设检验可能产生的两类错误;了解单个正态总体和两个正态总体的假设检验;了解总体分布函数的假设检验。 教学重点:单个正态和两个正态总体均值差的假设检验。 教学难点:p值法。 教学方法:讲授教学法、启发引导式教学法、讨论式教学法、习题讲解式教学法。 |
使学生掌握单个正态和两个正态总体均值差的假设检验。 |
五、各教学环节及学时分配
知识模块 |
教学内容 |
教学环节及学时 |
讲授课 |
习题课 |
讨论课 |
实验(实践) |
合计 |
第一章 概率 论 的基本概念 |
第1节 样本空间和随机事件 |
1 |
|
|
|
1 |
第2节 概率统计定义、古典概型,几何概型,公理化定义、性质 |
3 |
|
|
|
3 |
第3节 条件概率、全概率公式 |
2 |
|
|
|
2 |
第4节 事件的独立性、伯努利概型 |
2 |
|
|
|
2 |
第一章习题课 |
|
2 |
|
|
2 |
第二章随机变量 |
第1节 随机变量及其分布函数 |
1 |
|
|
|
1 |
第2节 离散型随机变量及其分布 |
2 |
|
|
|
2 |
第3节 连续型随机变量及其分布 |
2 |
|
|
|
2 |
第4节 随机变量函数的分布 |
2 |
|
|
|
2 |
第二章习题课 |
|
2 |
|
|
2 |
第三章 多维随机变量
|
第1节二维离散、连续随机变量及其分布 |
2 |
|
|
|
2 |
第2节边缘分布 |
2 |
|
|
|
2 |
第3节 条件分布 |
2 |
|
|
|
2 |
第4节 随机变量的独立性 |
2 |
|
|
|
2 |
第5节 两个随机变量函数的分布 |
2 |
|
|
|
2 |
第三章习题课 |
|
2 |
|
|
2 |
第四章 随机变量的数字特征
|
第1节 期望的定义、性质;g (X ) 的期望 |
2 |
|
|
|
2 |
第2节 方差的定义、性质及计算 |
2 |
|
|
|
2 |
第3节 协方差和相关系数的定义、性质 |
2 |
|
|
|
2 |
第4节 矩、协方差矩阵 |
1 |
|
|
|
1 |
第四章习题课 |
|
2 |
|
|
2 |
第五章大数定律与中心极限定理 |
第1节 大数定律 |
2 |
|
|
|
2 |
第2节 中心极限定理 |
2 |
|
|
|
2 |
第五章习题课 |
|
1 |
|
|
1 |
第六章数理统计的基本概念 |
第1节 随机样本 |
2 |
|
|
|
2 |
第2节 正态总体统计量及其分布 |
2 |
|
|
|
2 |
第六章习题课 |
|
1 |
|
|
1 |
第七章参数估计 |
第1节点估计 |
2 |
|
|
|
2 |
第2节估计量的评价标准 |
1 |
|
|
|
1 |
第3节 区间估计 |
2 |
|
|
|
2 |
第七章习题课 |
|
2 |
|
|
2 |
第八章假设检验 |
第1节 概述 |
1 |
|
|
|
1 |
第2节单个正态总体的假设检验 |
2 |
|
|
|
2 |
第八章习题课 |
|
2 |
|
|
2 |
总复习 |
|
|
2 |
|
|
2 |
合计 |
64 |
六、成绩考核及基本要求
考核 环节 |
建议分值 |
考核/评价细则 |
对应课程 目标 |
平时成绩 |
30% |
平时成绩包括出勤、作业和课堂表现。其中出勤占总成绩的10%,作业占总成绩的15%,课堂表现占总成绩的5%。 |
为了检验和改进学生的学习和教师的教学效果,改善课程设计,完善教学过程,有效促进学生的发展。 |
期末成绩 |
70% |
期末考试(闭卷)占总成绩的70%,课程总成绩按百分制记分,60分为及格。 |
通过复习,使学生对本学期所学的知识进行系统整理和复习,提高计算能力和解决问题的能力,发展统计观念,获得自身数学能力提高的成功体验,全面达到本学期规定的教学目标。 |
七、教材与主要教学参考资源
(一)教材
谢永钦主编,《概率论与数理统计》,北京邮电大学出版社,2017。
(二)主要教学参考资源
1. 张继昌编著,《概率论与数理统计教程》,浙江大学出版社,2008;
2. 沈恒范编著,《概率论与数理统计教程》(第四版),高等教育出版社,2003;
3. 茆诗松等编著,《概率论与数理统计教程》,高等教育出版社,2004;
4. 陈希孺编著,《概率论与数理统计》,中国科学技术大学出版社,2000;
5. 魏宗舒编著,《概率论与数理统计教程》,高等教育出版社,1983;
6. 王梓坤编著,《概率论基础及其应用》,高等教育出版社,1996;
7. 李贤平编著,《概率论基础》,高等教育出版社,1997;
8. 梁之舜等编著,《概率论与数理统计》(第三版),高等教育出版社,1988。
制定者:安徽燕
审核者:赵斐
批准者:高谦
编写时间:2022/6/16