1

一元函数部分补充

本章是对先修课程一元函数相关教学内容的补充，要求：理解海因定理的必要条件。理解并会运用夹逼准则和单调有界原理求极限。理解k阶无穷小的概念并会利用和差取大、和差代替、因式代替等规则求极限。理解并会用柯西定理、泰勒中值定理证明函数不等式。理解曲率和曲率半径的概念并掌握其计算方法。会求有理函数、三角函数有理式及简单无理函数的不定积分。理解积分限函数的概念，掌握其求导方法并会其证明积分等式。掌握常系数线性微分方程的基本知识和基本运算技能。

教学重点：运用极限存在准则求极限；常系数线性微分方程的基本知识和基本运算技能。

教学难点：海因定理；用柯西定理、泰勒中值定理证明函数不等式；积分限函数的求导。

教学方法：讲授教学法、启发引导式教学法、讨论式教学法、习题讲解式教学法。

使学生掌握一元函数中在极限计算及积分计算的技巧，理解并掌握一元函数微分学的应用，会求解高阶常系数线性微分方程。

2

多元函数部分补充

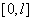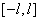本章是对先修课程多元函数相关教学内容的补充，要求：理解空间曲线的切线与法平面、曲面的切平面和法线、方向导数与梯度的概念并掌握其计算方法；掌握二重积分的应用，理解三重积分的概念；掌握三重积分的计算(直角坐标、柱坐标、球坐标)；会用三重积分计算简单的物理量——质心、.转动惯量、引力；理解两类曲线积分的概念，了解两类曲线积分的性质及两类曲线积分的关系；掌握计算两类曲线积分的方法；掌握格林公式并会运用平面曲线积分与路径无关的条件，会求全微分的原函数；理解两类曲面积分概念、性质及两类曲面积分的关系，掌握计算两类曲面积分的方法；理解高斯公式、斯托克斯公式，会用公式求一些几何量与物理量；会用曲线积分及曲面积分，求一些几何量与物理量(弧长、质量、功、转动惯量及流量等）；理解傅里叶级数的概念和函数展开为傅里叶级数的狄利克雷定理，会将定义在上的函数展开为正弦级数与余弦级数，会将定义在上的函数展开为傅里叶级数。

教学重点：三重积分的应用；对弧长的曲线积分；格林公式及应用；傅里叶级数。

教学难点：三重积分的计算；对面积的曲面积分；斯托克斯公式。

教学方法：讲授教学法、启发引导式教学法、讨论式教学法、习题讲解式教学法。

使学生掌握多元函数微分学和积分学的应用。掌握三重积分、曲线积分、曲面积分的计算和相互转化的方法，以及在几何和物理方面的应用。会根据需要将函数展开为傅里叶级数。

讲授课

习题课

讨论课

实验（实践）

合计

第一章

一元函数部分补充

1.1海因定理的必要条件

2

2

1.2再论极限存在准则

2

2

1.3无穷小的比较

2

2

1.4柯西中值定理

2

2

1.5泰勒中值定理

2

2

1.6函数不等式

2

2

1.7弧微分与曲率

2

2

1.8有理函数的不定积分

2

2

1.9积分限函数及积分等式证明

2

2

1.10常系数齐次线性微分方程

2

2

1.11常系数非齐次线性微分方程

2

2

第一章习题课

4

4

第二章

多元函数部分补充

2.1 多元函数微分学的几何应用

2

2

2.2方向导数与梯度

2

2

2.3条件极值及最值

2

2

2.4三重积分

2

2

2.5三重积分的应用

2

2

2.6对弧长的曲线积分

2

2

2.7对坐标的曲线积分

2

2

2.8格林公式及其应用

2

2.9对面积的曲面积分

2

2.10对坐标的曲面积分

2

2.11 高斯公式 通量与散

2

2.12斯托克斯公式 环流量与旋度

2

2.13傅里叶级数

2

2.14正弦级数 余弦级数

2

2.15一般周期函数的傅里叶级数

2

第二章习题课

6

6

总复习

2

2

合计

64

平时成绩

30%

共为30分，占总成绩的30%，其中出勤占总成绩的10%，作业占总成绩的15%，课堂表现占总成绩的5%。

全面检查学生对本学期所学知识的理解、掌握、运用及计算能力，提高数学水平。

期末考试

70%

期末考试半开卷，统一考试、批卷，满分为100分，按70%计入总成绩。

通过复习，使学生对本学期所学的知识进行系统整理和复习，提高计算能力和解决问题的能力，获得自身数学能力提高的成功体验，全面达到规定的教学目标。